The “n=leaf” Rose and Variations

By:

Alex Moore

In this investigation we explore polar coordinates and the “n-leaf” rose. Before we dive into mathematics fun we first review polar coordinates. Just like the standard x,y-plane is a coordinate system, polar coordinates is another coordinate system of the plane. To each point in the plane we assign an ordered pair (r,t) where r is the distance from the point to the origin and t is the angle of the line segment from the origin to the point, counterclockwise with respect to the x-axis. Here is a picture below: (we use t in place of theta for typing ease)

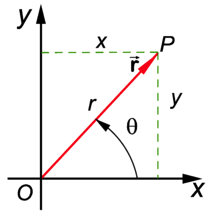
What is the relationship between our beloved x,y-coordinates and polar coordinates? Consider the point P above. Notice the dashed lines create right triangles. This allows us to use our basic trigonometry knowledge! Using trig, we see the length of the leg of the triangle along the x-axis is rcos(t) and the length of the leg of the triangle parallel to the y-axis is rsin(t). Thus, we have just “parametrized” the plane:

x = rcos(t);

y = rsin(t).

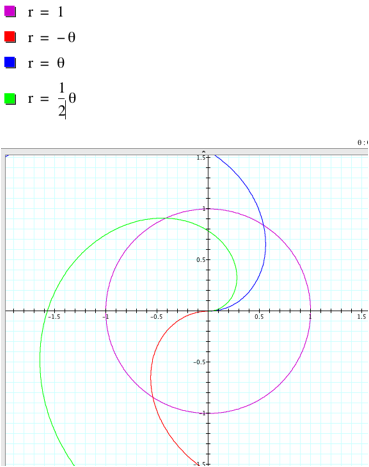
For function; we generally write r as a function of t, r(t), rather than y = f(x). Geometrically, this means that as we rotate counterclockwise around the origin the distance from the origin is changing depending on t. For example: consider the function r=1. This function represents the set of all points a distance 1 from the origin (as t changes, r stays constant at r=1), therefore r=1 is the unit circle. What about r=at for any real a? This says r grows with t at a linear rate:

Now that we have a basic feel for this new coordinate system we would like to investigate functions of the form r = a +b cos(n t). The simplest example is a=b=0 but this would mean r=0 and this is just one point: the origin. If we let b=0 then we get r=a and this is simply the circle centered at the origin of radius a. Now let us examine our first real example: let a=b be nonzero and let k be an integer. What happens? This!

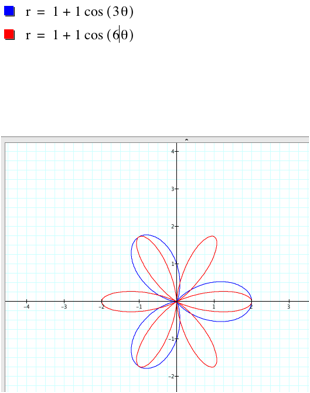
These graphs are the “3-leaf” and “6-leaf” roses. In general we call the graph of r=a(1+cos(k t)) the “n-leaf” rose, scaled by a factor of a. Nice pictures, eh? Lets alter this slightly. What if we ignore the 1, that is, what about the functions of the form r=a cos(k t)? Let us see using the same values of a and k in the previous example.

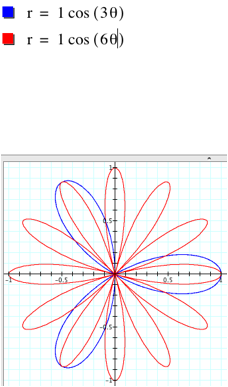
What changed? It “appears” that the blue graph didn’t change in the number of leaves and the red graph went from 6 leaves to 12 leaves. What actually happened to the blue graph is the graph repeated. If we let t run from only 0 to pi then we get the same graph. While the red graph needs t from 0 to 2pi to complete its 12 leaves the red graph needs only 0 to pi.

The reason we get nice, closed paths (leaves) is because the values for k are “nice.” These values are integers. If we let k be rational we get partial graphs (depending on the denominator). The most interesting case, in my opinion, is when we let k be an irrational number. If k is irrational then k t is a multiple of pi only when t=0. This means that r=a cos(k t) will never have a closed path. Speaking in topological terms, if we consider the set of all points (r,r(t)) with r then we get a dense subset of the unit disk! Here we graph for value of t between 0 and 100.

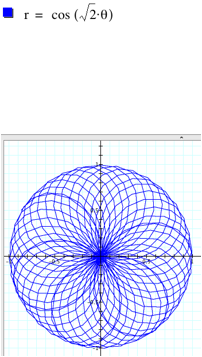
What changes if we use sin(k t) rather than cos(k t)? After some algebra,

r = a + bsin(k t) = a + bcos(k t – pi/2) = a + bcos(k(t-pi/2k)) = a + bcos(k t’), where t’=t-pi/2k.

Using this change of variables we see that the graphs of these two functions are just rotations of one another! This should not be surprising to us given the nature of sine and cosine and the relationship between them, sin(t)=cos(t-pi/2).